상호 배타적 집합
어떤 학교에 N명의 사람이 있다고 가정해보자.
학교에서 이 사람들은 처음에는 흩어져 있다가,
서로 같은 학과임을 확인하면 같이 그룹을 만든다.
만약 두 그룹이 서로가 같은 학과임을 확인하면 두 그룹을 합한 더 큰 그룹을 만든다.
이 상황을 표현하기 위해 사용되는 개념이 상호 배타적 집합(서로소 집합)이다.

상호 배타적 집합은 흩어져 있는 원소들을 묶어서 표현한다.
중요한 점은, 이 집합에서는 서로 다른 두 집합에 대해서 교집합이 생기는 상황을 가정하지 않는다.
즉 교집합이 있다면, 그것은 상호배타적 집합이라 할 수 없다.
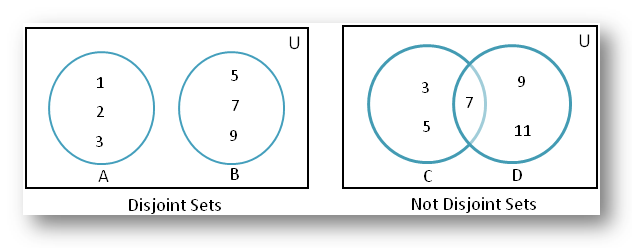
이것을 알고리즘으로 표현하려면 어떻게 해야 할까?
상호 배타적 집합을 표현하기 위해서는 기본적으로 다음과 같은 연산들이 필요하다.
Find : 어떤 원소가 속한 그룹을 알아내는 연산
Union : 두 그룹을 합치는 연산
가장 먼저 배열로 구현한다고 가정해보자.
group[n]이라는 n 크기의 배열을 각 원소들의 그룹 번호를 저장하는 용도로 이용해보자.
group[i] i번 원소의 그룹 번호를 지정한다.
이렇게 하면, i번 원소가 어느 그룹에 속한지 알아내는것은 (Find 연산) O(1) 시간에 가능하다.
하지만 두 그룹을 합치기 위해서는(Union 연산) O(N)의 시간이 필요하다.
index 0 1 2 3 4
group number 1 1 1 2 2
2번 그룹을 1번 그룹에 합친 후,
index 0 1 2 3 4
group number 1 1 1 1 1
그러므로 배열로 구현하는것은 부적절하다.
리스트는 어떨까?
n개의 리스트를 각각 원소가 하나인 그룹으로 두고 시작해보자.
그룹을 합치는 상황에 하나의 리스트를 다른 리스트의 꼬리에 붙인다.
이렇게 한다면 두 그룹을 합치기 위해 O(1) 시간이면 충분하다.
하지만 이 경우, 오히려 Find를 수행할 때 문제가 생긴다.
어느정도 그룹이 형성된 리스트들 속에서 어떤 원소가 어느 리스트에 속해있는지 알기 위해서는 O(N) 시간이 필요하다.
그 외 다른 일반적인 자료구조(이진트리, 해시테이블 등)를 이용하더라도 합치는 연산을 효과적으로 수행하기는 어렵다.
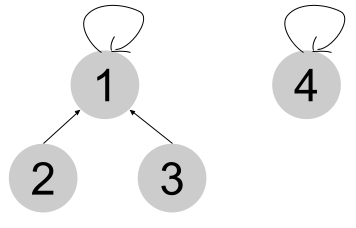
다음으로 트리를 이용한다고 가정해보자.
각각의 집합을 하나의 루트를 갖는 트리로 대응시켜보자.
모든 원소들이 자신의 부모노드를 참조할 수 있다면 (자신이 루트라면 자기자신을 참조),
모든 원소들은 자신의 루트를 알아낼 수 있고,
이 루트를 각 그룹의 id로 사용할 수 있을 것이다.
그렇다면, Find 연산은 해당 원소의 루트를 찾는 방법으로 구현하면 된다.
그리고 Union 연산은 두 원소들의 루트를 찾고,
한쪽 루트가 다른쪽 루트를 부모로 참조하도록 하면 될 것이다.
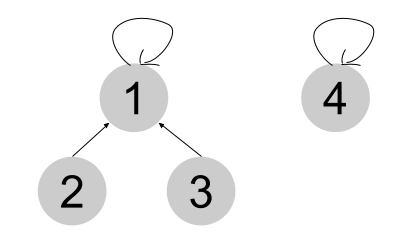
구현
각 원소의 부모 원소가 저장될 parent 배열을 정의한다.
Init
시작 시, 모든 원소는 각각이 유일한 집합으로 표현된다.
그러므로 각 원소들을 모두 루트이고, parent로 자기자신을 참조한다.
Find
어떤 원소가 속한 집합을 알기 위해, 해당 원소의 루트 번호를 찾는다.
parent 배열을 거슬러 올라가면 루트 번호에 도달하게 된다.
그러므로, 같은 트리에 있는 모든 원소들은 같은 루트 번호를 반환하게 된다.
이렇게 설계한다면 트리가 균형 잡혀있는 경우 O(logN) 시간에 Find 연산을 수행할 수 있다.
Find(1)
1번 원소의 루트 : 1
1 -> 1
Find(2)
2번 원소의 루트 : 1
2 -> 1
Find(3)
3번 원소의 루트 : 1
3 -> 1
Find(4)
4번 원소의 루트 : 1
4 -> 3 -> 1
Union
어떤 두 원소를 합치기 위해,
두 원소가 속한 두 집합의 루트 번호를 찾고,
두 집합이 서로 다른 집합이라면 (루트 번호가 다르다면),
한쪽 루트가 다른쪽 루트를 부모로 참조한다.
그러면 집합이 합쳐진다.
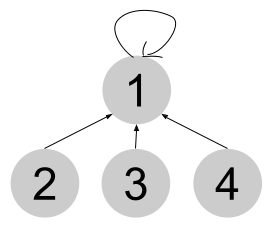
Union(2, 4)를 예로 들어보자
Find(2) = 1
Find(4) = 4
4 != 1 이므로 2번 원소와 4번 원소는 서로 다른 집합에 속한다.
4번 집합의 루트가 1번 집합의 루트를 부모로 갖도록 하여 두 집합을 합친다.
이렇게 설계한다면, 두 집합을 합치는 연산은 Find의 비용과 동일하게 O(logN)이다.
소스코드
github.com/insooneelife/AlgorithmTutorial/blob/master/Algorithm/Sources/UnionFind/1-Union-Find.cpp
insooneelife/AlgorithmTutorial
알고리즘 튜토리얼. Contribute to insooneelife/AlgorithmTutorial development by creating an account on GitHub.
github.com
랭크를 이용한 최적화 구현
트리를 이용하여 자료구조를 설계하면 O(logN)의 성능으로 Find와 Union이 둘 다 가능하다.
하지만 이 성능은 트리가 균형 잡혀있는 경우에만 해당된다.
만약 트리가 한쪽으로 완전하게 치우쳐져 있다면, 배열과 크게 다를 것이 없을 것이다.
이 문제를 피하기 위해,
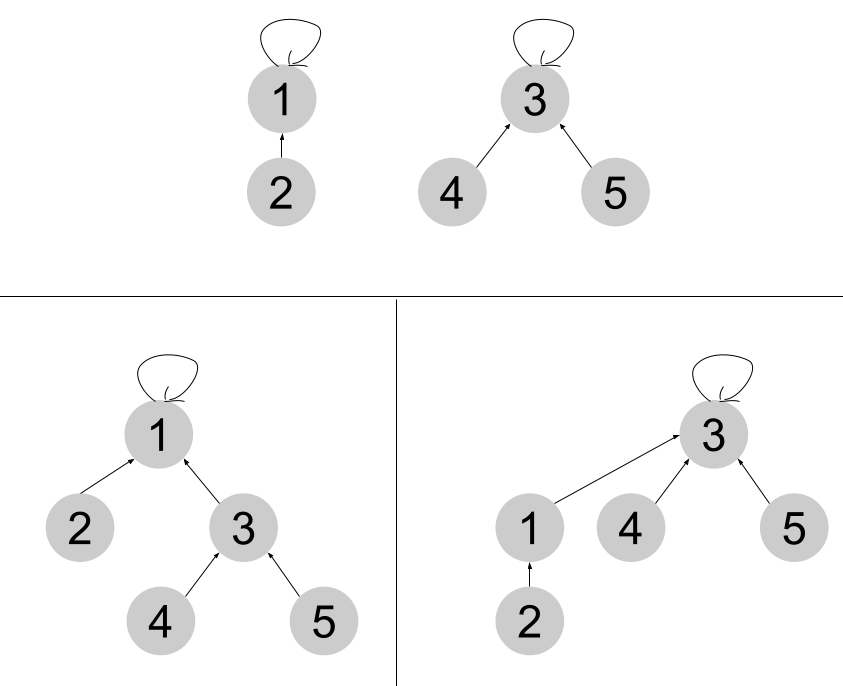
트리의 높이를 비교하여 낮은쪽 트리를 높은쪽 트리에 붙이는 전략을 사용할 수 있다.
이러한 전략을 랭크에 의한 합치기(Union by Rank)라고 부른다.
이 전략을 통해 합치기 연산을 한다면, 높이가 1인 {3}이 높이가 2인 {1, 2}에 합쳐질 것이다.
그리고 이렇게 합쳐진다면, 기존에 합쳐지던 방식보다 훨씬 더 트리를 균형있게 유지할 수 있다.

만약 높이가 같은 두 트리를 합치면 어떻게 될까?
어느쪽에 붙여도 상관없다.
트리의 높이는 어떤 식으로든 1 증가하게 될 것이다.
소스코드
insooneelife/AlgorithmTutorial
알고리즘 튜토리얼. Contribute to insooneelife/AlgorithmTutorial development by creating an account on GitHub.
github.com
경로 압축을 통한 최적화 구현
많은 경우 랭크 최적화만으로도 충분하지만, 간단하면서도 아주 큰 효과가 있는 최적화 방법이 하나 더 있다.
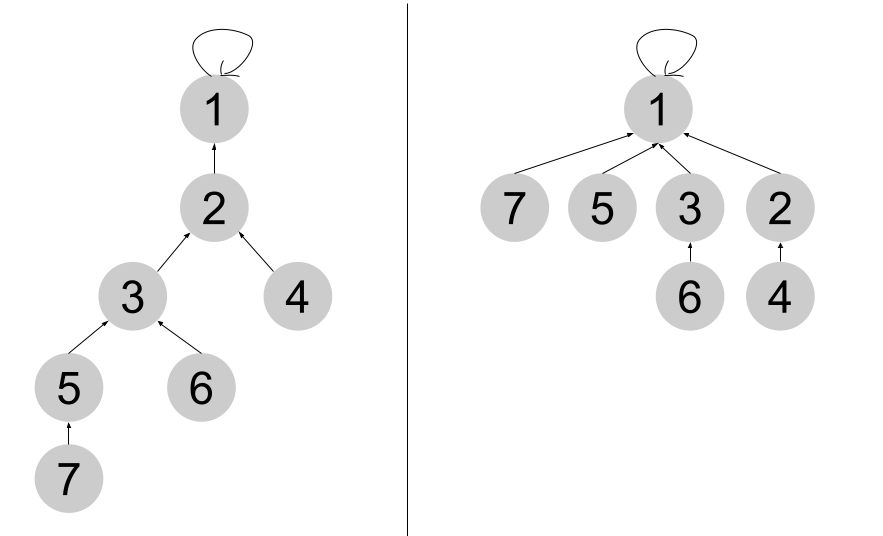
이 최적화는 Find 연산이 중복된 계산을 여러 번 하고 있다는 데 착안한다.
Find(n) 연산을 통해 n이 속한 트리의 루트를 찾아냈다고 하자.
이때 parent[n]를 찾아낸 루트로 아예 바꿔버리는 것이다.
그렇게 되면 다음번 Find(n) 부터는 더이상 거슬러 올라가는 과정 없이 바로 루트를 찾아올 수 있다.
또한 Find함수를 재귀적으로 구현하였기 때문에, 거슬러 올라가는 과정에 있는 모든 원소들은 가장 상단에 있는 루트를 바라보게 될 것이다. 즉 Find를 하면 할 수록 점점 더 성능이 좋아지게 된다.
(Union 함수도 내부적으로 Find를 호출하기 때문에 마찬가지로 호출 시 자료구조의 성능이 좋아진다.)
호출이 지속되는 경우 시간복잡도는 O(a(N))에 수렴하고, 이 값은 상수값(4 이하)으로 봐도 무방하다.
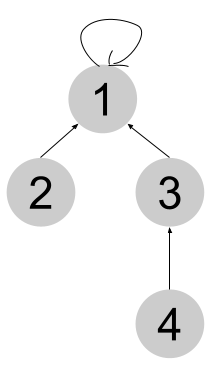
다음 왼쪽 그림에서 Find(7)을 수행하면, 오른쪽처럼 된다.
소스코드
다음 코드를,
int Find(int i) const
{
if (i == parent[i]) return i;
return Find(parent[i]);
}다음 코드로 수정하면 된다.
int Find(int i)
{
if (i == parent[i]) return i;
return parent[i] = Find(parent[i]);
}
연습 문제로 다음 문제를 풀어보자.
https://programmers.co.kr/learn/courses/30/lessons/42861
코딩테스트 연습 - 섬 연결하기
4 [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] 4
programmers.co.kr
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [Algorithm] 비트마스크 (0) | 2021.05.11 |
|---|---|
| [Algorithm] 프로그래머스 - 2019 카카오 개발자 겨울 인턴십 풀이 (0) | 2021.05.08 |
| [Algorithm] 프로그래머스 - 2019 KAKAO BLIND RECRUITMENT 풀이 (0) | 2021.05.05 |
| [Algorithm] 프로그래머스 - 2020 KAKAO BLIND RECRUITMENT 풀이 (0) | 2021.05.02 |
| [Algorithm] Hash Table vs Binary Search Tree 비교 (0) | 2021.04.29 |
상호 배타적 집합
어떤 학교에 N명의 사람이 있다고 가정해보자.
학교에서 이 사람들은 처음에는 흩어져 있다가,
서로 같은 학과임을 확인하면 같이 그룹을 만든다.
만약 두 그룹이 서로가 같은 학과임을 확인하면 두 그룹을 합한 더 큰 그룹을 만든다.
이 상황을 표현하기 위해 사용되는 개념이 상호 배타적 집합(서로소 집합)이다.

상호 배타적 집합은 흩어져 있는 원소들을 묶어서 표현한다.
중요한 점은, 이 집합에서는 서로 다른 두 집합에 대해서 교집합이 생기는 상황을 가정하지 않는다.
즉 교집합이 있다면, 그것은 상호배타적 집합이라 할 수 없다.

이것을 알고리즘으로 표현하려면 어떻게 해야 할까?
상호 배타적 집합을 표현하기 위해서는 기본적으로 다음과 같은 연산들이 필요하다.
Find : 어떤 원소가 속한 그룹을 알아내는 연산
Union : 두 그룹을 합치는 연산
가장 먼저 배열로 구현한다고 가정해보자.
group[n]이라는 n 크기의 배열을 각 원소들의 그룹 번호를 저장하는 용도로 이용해보자.
group[i] i번 원소의 그룹 번호를 지정한다.
이렇게 하면, i번 원소가 어느 그룹에 속한지 알아내는것은 (Find 연산) O(1) 시간에 가능하다.
하지만 두 그룹을 합치기 위해서는(Union 연산) O(N)의 시간이 필요하다.
index 0 1 2 3 4
group number 1 1 1 2 2
2번 그룹을 1번 그룹에 합친 후,
index 0 1 2 3 4
group number 1 1 1 1 1
그러므로 배열로 구현하는것은 부적절하다.
리스트는 어떨까?
n개의 리스트를 각각 원소가 하나인 그룹으로 두고 시작해보자.
그룹을 합치는 상황에 하나의 리스트를 다른 리스트의 꼬리에 붙인다.
이렇게 한다면 두 그룹을 합치기 위해 O(1) 시간이면 충분하다.
하지만 이 경우, 오히려 Find를 수행할 때 문제가 생긴다.
어느정도 그룹이 형성된 리스트들 속에서 어떤 원소가 어느 리스트에 속해있는지 알기 위해서는 O(N) 시간이 필요하다.
그 외 다른 일반적인 자료구조(이진트리, 해시테이블 등)를 이용하더라도 합치는 연산을 효과적으로 수행하기는 어렵다.
다음으로 트리를 이용한다고 가정해보자.
각각의 집합을 하나의 루트를 갖는 트리로 대응시켜보자.
모든 원소들이 자신의 부모노드를 참조할 수 있다면 (자신이 루트라면 자기자신을 참조),
모든 원소들은 자신의 루트를 알아낼 수 있고,
이 루트를 각 그룹의 id로 사용할 수 있을 것이다.
그렇다면, Find 연산은 해당 원소의 루트를 찾는 방법으로 구현하면 된다.
그리고 Union 연산은 두 원소들의 루트를 찾고,
한쪽 루트가 다른쪽 루트를 부모로 참조하도록 하면 될 것이다.

구현
각 원소의 부모 원소가 저장될 parent 배열을 정의한다.
Init
시작 시, 모든 원소는 각각이 유일한 집합으로 표현된다.
그러므로 각 원소들을 모두 루트이고, parent로 자기자신을 참조한다.

Find
어떤 원소가 속한 집합을 알기 위해, 해당 원소의 루트 번호를 찾는다.
parent 배열을 거슬러 올라가면 루트 번호에 도달하게 된다.
그러므로, 같은 트리에 있는 모든 원소들은 같은 루트 번호를 반환하게 된다.
이렇게 설계한다면 트리가 균형 잡혀있는 경우 O(logN) 시간에 Find 연산을 수행할 수 있다.

Find(1)
1번 원소의 루트 : 1
1 -> 1
Find(2)
2번 원소의 루트 : 1
2 -> 1
Find(3)
3번 원소의 루트 : 1
3 -> 1
Find(4)
4번 원소의 루트 : 1
4 -> 3 -> 1
Union
어떤 두 원소를 합치기 위해,
두 원소가 속한 두 집합의 루트 번호를 찾고,
두 집합이 서로 다른 집합이라면 (루트 번호가 다르다면),
한쪽 루트가 다른쪽 루트를 부모로 참조한다.
그러면 집합이 합쳐진다.
Union(2, 4)를 예로 들어보자
Find(2) = 1
Find(4) = 4
4 != 1 이므로 2번 원소와 4번 원소는 서로 다른 집합에 속한다.
4번 집합의 루트가 1번 집합의 루트를 부모로 갖도록 하여 두 집합을 합친다.
이렇게 설계한다면, 두 집합을 합치는 연산은 Find의 비용과 동일하게 O(logN)이다.


소스코드
github.com/insooneelife/AlgorithmTutorial/blob/master/Algorithm/Sources/UnionFind/1-Union-Find.cpp
insooneelife/AlgorithmTutorial
알고리즘 튜토리얼. Contribute to insooneelife/AlgorithmTutorial development by creating an account on GitHub.
github.com
랭크를 이용한 최적화 구현
트리를 이용하여 자료구조를 설계하면 O(logN)의 성능으로 Find와 Union이 둘 다 가능하다.
하지만 이 성능은 트리가 균형 잡혀있는 경우에만 해당된다.
만약 트리가 한쪽으로 완전하게 치우쳐져 있다면, 배열과 크게 다를 것이 없을 것이다.
이 문제를 피하기 위해,
트리의 높이를 비교하여 낮은쪽 트리를 높은쪽 트리에 붙이는 전략을 사용할 수 있다.
이러한 전략을 랭크에 의한 합치기(Union by Rank)라고 부른다.
이 전략을 통해 합치기 연산을 한다면, 높이가 1인 {3}이 높이가 2인 {1, 2}에 합쳐질 것이다.
그리고 이렇게 합쳐진다면, 기존에 합쳐지던 방식보다 훨씬 더 트리를 균형있게 유지할 수 있다.

만약 높이가 같은 두 트리를 합치면 어떻게 될까?
어느쪽에 붙여도 상관없다.
트리의 높이는 어떤 식으로든 1 증가하게 될 것이다.

소스코드
insooneelife/AlgorithmTutorial
알고리즘 튜토리얼. Contribute to insooneelife/AlgorithmTutorial development by creating an account on GitHub.
github.com
경로 압축을 통한 최적화 구현
많은 경우 랭크 최적화만으로도 충분하지만, 간단하면서도 아주 큰 효과가 있는 최적화 방법이 하나 더 있다.
이 최적화는 Find 연산이 중복된 계산을 여러 번 하고 있다는 데 착안한다.
Find(n) 연산을 통해 n이 속한 트리의 루트를 찾아냈다고 하자.
이때 parent[n]를 찾아낸 루트로 아예 바꿔버리는 것이다.
그렇게 되면 다음번 Find(n) 부터는 더이상 거슬러 올라가는 과정 없이 바로 루트를 찾아올 수 있다.
또한 Find함수를 재귀적으로 구현하였기 때문에, 거슬러 올라가는 과정에 있는 모든 원소들은 가장 상단에 있는 루트를 바라보게 될 것이다. 즉 Find를 하면 할 수록 점점 더 성능이 좋아지게 된다.
(Union 함수도 내부적으로 Find를 호출하기 때문에 마찬가지로 호출 시 자료구조의 성능이 좋아진다.)
호출이 지속되는 경우 시간복잡도는 O(a(N))에 수렴하고, 이 값은 상수값(4 이하)으로 봐도 무방하다.
다음 왼쪽 그림에서 Find(7)을 수행하면, 오른쪽처럼 된다.

소스코드
다음 코드를,
int Find(int i) const
{
if (i == parent[i]) return i;
return Find(parent[i]);
}다음 코드로 수정하면 된다.
int Find(int i)
{
if (i == parent[i]) return i;
return parent[i] = Find(parent[i]);
}
연습 문제로 다음 문제를 풀어보자.
https://programmers.co.kr/learn/courses/30/lessons/42861
코딩테스트 연습 - 섬 연결하기
4 [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] 4
programmers.co.kr
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [Algorithm] 비트마스크 (0) | 2021.05.11 |
|---|---|
| [Algorithm] 프로그래머스 - 2019 카카오 개발자 겨울 인턴십 풀이 (0) | 2021.05.08 |
| [Algorithm] 프로그래머스 - 2019 KAKAO BLIND RECRUITMENT 풀이 (0) | 2021.05.05 |
| [Algorithm] 프로그래머스 - 2020 KAKAO BLIND RECRUITMENT 풀이 (0) | 2021.05.02 |
| [Algorithm] Hash Table vs Binary Search Tree 비교 (0) | 2021.04.29 |
