재귀 함수
컴퓨터가 수행하는 대부분의 작업들은 좀 더 작은 단위의 작업들로 나누어 볼 수 있다.
예를 들어 온라인으로 상품을 구매하는 작업은, 상품 정보 조회하기, 구매자 정보 조회하기, 구매자-상품 결제 처리하기, 데이터베이스 갱신하기, 문자 보내기 와 같은 더 작은 단위의 작업들로 나누어진다.
또 그 중에서 상품 정보 조회하기와 같은 작업은, 자료구조에 따라 다르겠지만, 상품 정보를 비교하는 작업을 반복적으로 수행하여 정보를 찾게 된다. 이렇게 어떤 작업들을 더 작은 작업들로 표현할 수 있는데, 이 범위가 작아지면 작아질수록 작업의 형태가 유사해지게 된다. 이런 상황을 코드로 구현할 때 유용하게 사용되는 개념이 바로 재귀 함수이다.
재귀적 정의
재귀 함수란 수행해야하는 목표 작업을 유사한 형태의 조각으로 쪼갠 후 그 중 한 조각을 수행하고,
나머지 작업에 대해 다시 목표 작업을 호출해 실행하는 함수를 의미한다.
즉 자기 자신의 문제를 해결하기 위해 자기 자신을 재귀적으로 이용하는 것이다.
1부터 N까지의 합을 구하는 함수를 재귀 함수를 이용하여 구현해보자.
int Sum(int n)
{
if (n == 1)
return 1;
return Sum(n - 1) + n;
}
이 코드를 보면, 전체 목표 작업인 [1,N] 까지의 합을 N + [1, N-1] 까지의 합의 형태로 분할하여 정의한 것을 확인할 수 있다. N이라는 값을 더하는 부분이 쪼개진 한 조각이고, 나머지 [1, N-1]은 다시 자기자신의 형태를 빌려 Sum(n - 1)로 표현한다. 이 코드는 다음과 같은 그림으로 호출된다.
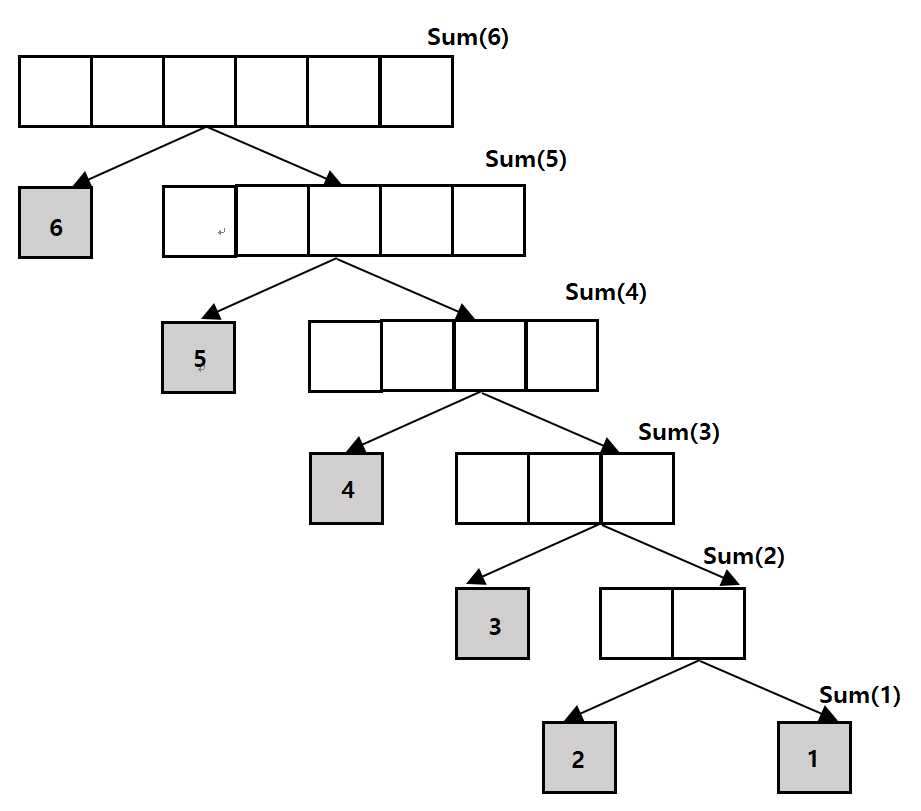
기저 조건
재귀 함수를 구현하기 위해 또 알아둬야하는 부분은 기저 조건이다. 재귀 함수는 자기 자신을 다시 호출한다는 점에서 문제를 쉽게 해결하는 도구가 되기도 하지만, 이러한 특성 때문에 영원히 함수호출을 하게 될 수도 있다.
(함수 호출을 끊임없이 반복하는 경우, 함수 호출 스택이 가득 차 버리는데 이 문제를 Stack Overflow라고 부른다.)
문제가 적당히 작아져서 바로 답을 구할 수 있는 상황에 대해 빈틈없는 기저 조건을 정의하고, 그 단계에서 호출의 고리를 끊어줘야 최종적으로 재귀함수의 구현이 완결될 것이다.
꼬리 재귀 (Tail Recursion)
재귀 함수에서 또 자주 등장하는 개념으로, 꼬리 재귀라는 것이 있다.
일반적으로 다음 함수를 호출하게 되면, 기저 조건을 만날때까지 함수가 반복적으로 호출될 것이고,
함수 호출 스택에는 문제가 완결될 때까지 메모리가 쌓이게 될 것이다.
int Sum(int n)
{
if (n == 1)
return 1;
return Sum(n - 1) + n;
}
하지만 이 코드를 다음과 같이 바꾸면 어떻게 될까?
int SumTR(int n, int ans)
{
if (n == 0)
return ans;
return SumTR(n - 1, n + ans);
}
// interface
int SumTR(int n)
{
return SumTR(n, 0);
}운영체제는 함수의 끝 이후 더 이상 할 작업이 없음을 알기 때문에, 호출스택을 비운 후 다시 재귀호출을 수행하게 된다.
즉 호출스택이 쌓이지 않게 되고, 또한 이런 형태의 재귀는 컴파일러 최적화를 통해 반복문과 비슷한 수준까지 최적화가 가능하게 된다. 그러므로 꼬리재귀를 활용할 수 있다면, 성능, 메모리 모든 면에서 이점을 얻을 수 있다.
참고로 요즘 컴파일러는 다음과 같은 형태의 코드도 꼬리재귀로 최적화를 수행해준다.
int Sum(int n)
{
if (n == 1)
return 1;
return n + Sum(n - 1);
}
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [Algorithm] 트라이 (0) | 2021.06.12 |
|---|---|
| [Algorithm] 동적계획법 (0) | 2021.05.30 |
| [Algorithm] 분할 정복 (2) | 2021.05.26 |
| [Algorithm] 상태 공간 탐색 (0) | 2021.05.20 |
| [Algorithm] 시뮬레이션, 구현 (0) | 2021.05.15 |
