[Algorithm] 부분합

부분합

다음과 같은 수열이 있다.

v = {2, 3, 7, 5}

이 수열에서 구간 [1, 3]의 합은 3 + 7 + 5 = 15 이다.

이처럼 어떤 임의의 구간 [i, j]가 주어졌을 때,

구간의 합을 구하기 위해서는 해당 구간을 순회하며 값을 더하면 될 것이다.

하지만 만약 수열의 크기 N이 크고 이런 구간에 대한 질의 개수 Q도 많아진다면 어떻게 될까?

위와 같은 방식으로는 최악의 경우 O(N x Q) 의 시간복잡도를 갖게 될 것이다.

이러한 문제를 해결하기 위해 고안된 방법으로 부분합(Partial Sum or Prefix Sum)이 있다.

 

부분합은 배열 원소의 인덱스까지의 합으로 다음과 같이 정의된다.

psum[i] = ∑ v[k]  (0<=k<=i)

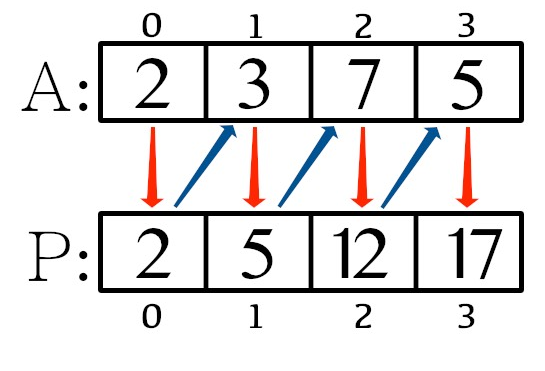
v =	{2, 3, 7, 5}
psum =	{2, 5, 12, 17}

 

 

이처럼 각 원소의 인덱스까지의 합을 미리 계산해둔 배열이 있다면 이제 구간에 대한 합을 쉽게 표현할 수 있다.
구간 [i, j]의 원소들의 합 : psum[j] - psum[i - 1]
위에서 언급한 구간 [1, 3]의 합은 psum[3] - psum[0] 으로 이 값을 계산하면 15 이다.
만약 [0, 2]와 같은 구간이 들어온다면 어떻게 될까?? 
psum[2] - psum[-1]로 표현되기 때문에 인덱스를 벗어나는 문제가 생길 수 있는데,
인덱스 -1은 0으로 예외처리를 해주어도 되고, 배열을 한칸 더 잡고 가장 앞의 원소를 0으로 두는 방법도 가능하다.

중요한 점은, 이처럼 미리 각 인덱스까지의 합을 계산해둔 psum 배열이 있다면, 언제든지 두 배열값의 차를 이용하여 빠르게 구간에 대한 합을 구할 수 있다는 것이다. 이 방법을 이용한다면 수열의 크기와 구간에 대한 쿼리가 모두 많은 문제에 대해서 O(N + Q) 시간에 동작한다.

 

소스코드

https://github.com/insooneelife/AlgorithmTutorial/blob/master/Algorithm/Sources/PartialSum/1-PartialSum.cpp

insooneelife/AlgorithmTutorial

 

2차원 부분합

부분 합은 1차원 배열에서만 사용가능한 것은 아니다. 2차원 배열 A[][]가 주어질 때,

이 배열에서 y1, x1 인덱스 위치부터 y2, x2 인덱스 위치까지 직사각형 구간의 합을 계산해야 한다고 가정해보자.

이 문제는 다음과 같은 2차원 부분합 배열을 이용하면 빠르게 계산할 수 있다.

psum[y][x] = ∑ ∑ A[i][j]  (0<=i<=y) (0<=j<=x)

즉, 이 psum[y][x]는 왼쪽 위 (0, 0)부터 오른쪽 아래 (y, x) 까지의 직사각형 구간의 원소들의 합을 모두 더한 값이다.

이렇게 모든 (0, 0) 부터 임의의 (y, x) 직사각형 구간에 대한 합을 갖고 있다면,

임의의 (y1, x1) 부터 임의의 (y2, x2) 직사각형 구간에 대한 합도 쉽게 계산할 수 있다.

다음 그림을 참고하자.

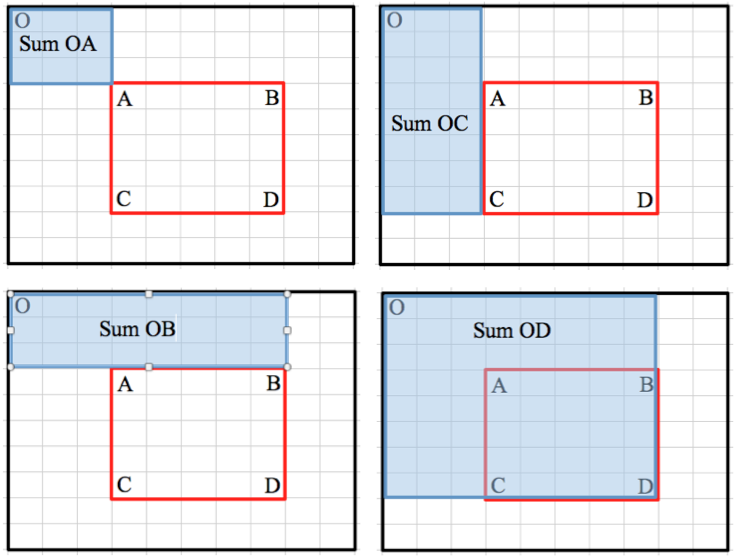
그림처럼 위치 O(0, 0) 부터 위치 D까지의 직사각형 구간의 합 Sum OD에서,

O부터 B까지의 합 Sum OB와, O부터 C까지의 합 Sum OC를 뺀다면,

O부터 A까지의 합 Sum OA는 두 번 지워지게 된다.

그러므로 마지막에 Sum OA를 더해준다면, 임의의 직사각형 구간에 대한 구간합을 구할 수 있다.

Sum(y1, x1, y2, x2) = psum[y2][x2] - psum[y2][x1 - 1] - psum[y1 - 1][x2] + psum[y1 - 1][x1 - 1]

 

소스코드

https://github.com/insooneelife/AlgorithmTutorial/blob/master/Algorithm/Sources/PartialSum/2-PartialSum2D.cpp

insooneelife/AlgorithmTutorial

 

최대 누적 구간 찾기

부분합을 활용한 문제 중에서 또 자주 등장하는 문제는 최대 누적 구간을 찾는 형태의 문제들이다.

다음과 같은 문제를 생각해보자.

어떤 공원에 N명의 사람들이 찾아온다고 가정하자.

이 사람들이 공원을 찾아오는 시간과 떠나는 시간은 항상 일정하다.

여기서 한 시간 정도의 구간동안 공원에 사람이 가장 많이 몰리는 시간대를 찾으려고 한다.

사람이 몰리는 정도는 (시간구간의 길이 * 그 시간대에 공원에 있던 사람수) 로 정의한다.

예를 들어 00:00-00:29까지 2명, 00:30-00:59까지 1명이었다고 하면,

한 시간 구간동안 사람이 몰리는 정도는 30 * 2 + 30 * 1 = 90이 된다.

 

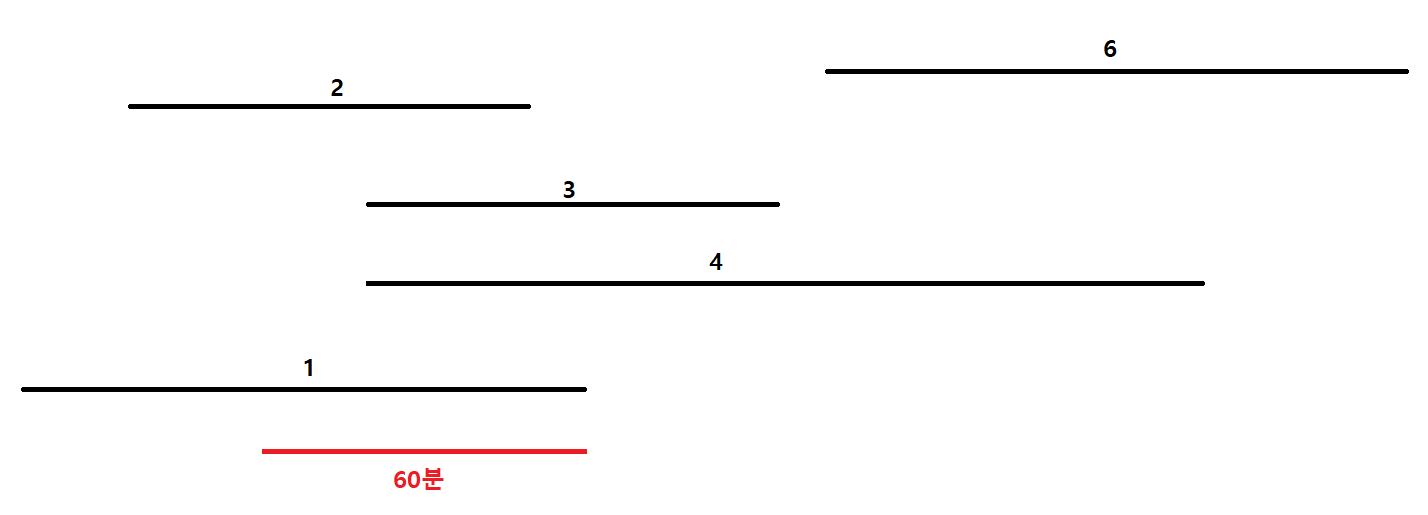
이 문제에서는 시청자들이 가장 많이 몰리는 1시간짜리 구간을 찾아야하는데, 부분합을 이용한다면 이런 형태의 문제를 쉽게 해결할 수 있다. 먼저 분 단위 모든 타임라인에 대한 배열을 생성한다.

vector<long long> psum(1440, 0);

 

그 후 각 분 단위로 몇명의 사람들이 공원에 있었는지를 타임라인에 저장한다.

이 부분에서 모든 사람들의 시간 시간부터 끝 시간까지를 루프를 이용하여 누적시킨다면 시간초과가 날 수 있다.

여기서 누적합을 활용한 꽤 유용한 방법이 있는데, 시작시간은 +1, 퇴장시간은 -1로 초기화한 후 그 값에 대해 부분합을 만드는 것이다. 예를 들어 어떤 사람이 1시에 입장해서 2시에 퇴장하였다면 다음과 같이 처리한다.

vector<long long> psum(1440, 0);
psum[60] = 1;
psum[120] = -1;

for (int i = 1; i < 1440; ++i)
{
	psum[i] += psum[i - 1];
}

그러면 다음과 같은 누적합이 만들어진다.

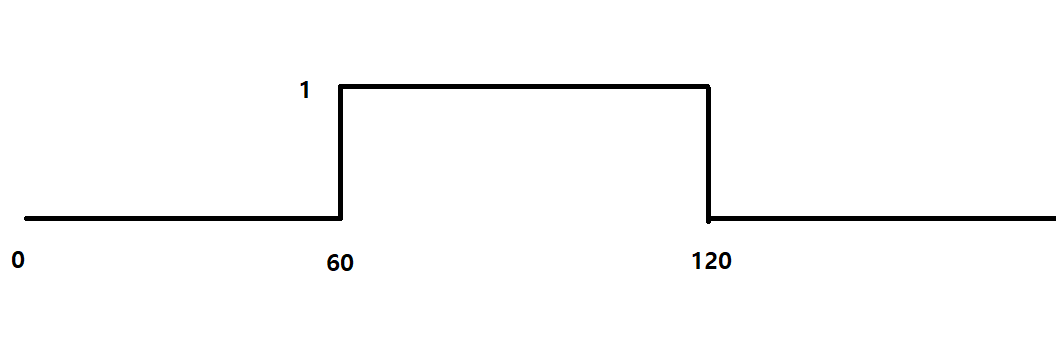
이 작업은 모든 사람들의 입장시간을 +1, 퇴장시간을 -1 로 초기화한 후 처리하여도 완벽하게 동작한다.

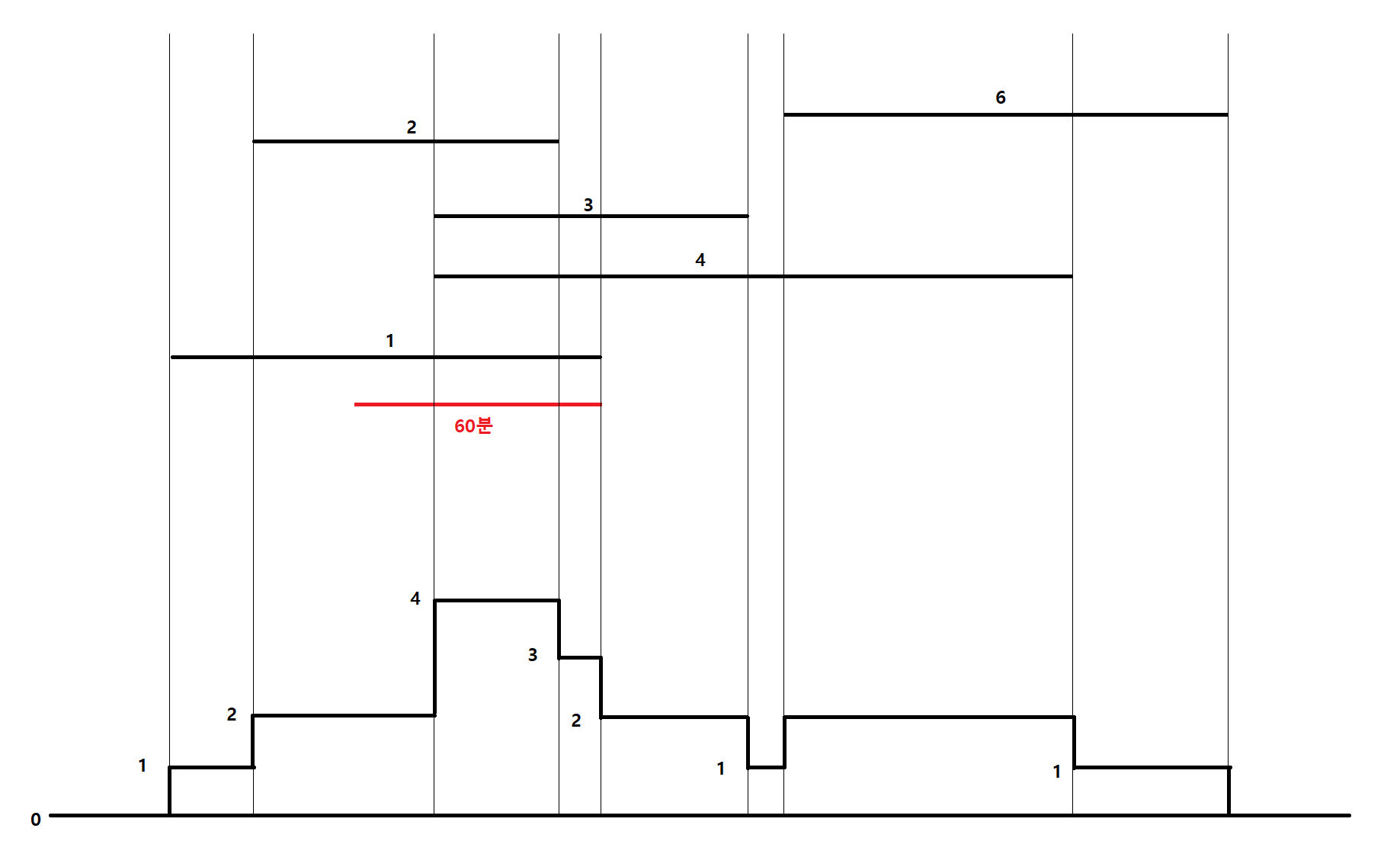
여기까지 작업이 되었다면 psum에는 각 분 단위로 몇명이 공원에 있는지를 저장하고 있을 것이다.

그렇다면 여기서 임의의 구간동안 가장 많은 사람이 몰리는 위치를 찾으려면 어떻게 해야할까?

먼저 각 구간에 누적합에 대한 질의를 빠르게 수행하도록 하기 위해 모든 타임라인에 대한 부분합을 만들어야한다.

부분합을 만들기 위해, 위의 누적합 처리를 통해 만들어진 psum 배열을 한 번 더 누적시킨다.

for (int i = 1; i < 1440; ++i)
{
	psum[i] += psum[i - 1];
}

 

타임라인에 대한 부분합이 만들어졌다면, 이제 각 구간에 대한 누적합을 빠르게 계산할 수 있다.

예를 들어 파란색 구간의 누적합을 구하고 싶은 경우 psum[280] - psum[220]을 통해 쉽게 계산해낼 수 있다.

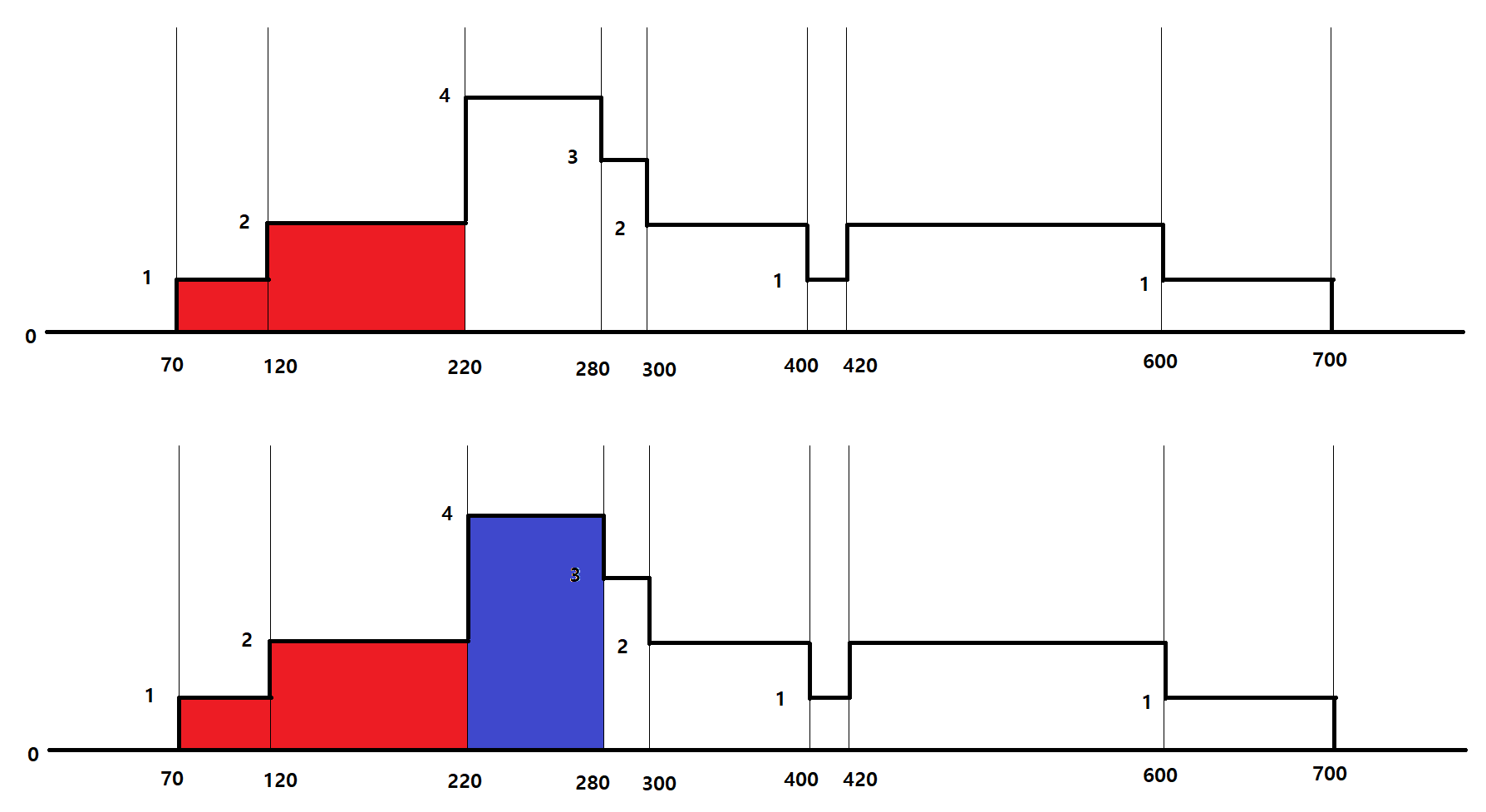
이제 한 시간동안의 가장 큰 누적구간을 찾기 위해 타임라인의 모든 분을 시작점으로 psum[i] - psum[i - 60]이 최대가 되는 위치를 찾으면 된다.