오일러 경로
오일러 경로(Eulerian Trail)은 그래프에 존재하는 모든 간선을 정확히 한 번씩 방문하는 연속된 경로를 의미한다.

시작점을 어느 지점으로 하느냐에 따라 몇몇의 간선에 도달하지 못할수도 있다.

오일러 회로
오일러 회로(Eulerian Circuit)은 시작점과 끝점이 같은 오일러 경로를 의미한다.
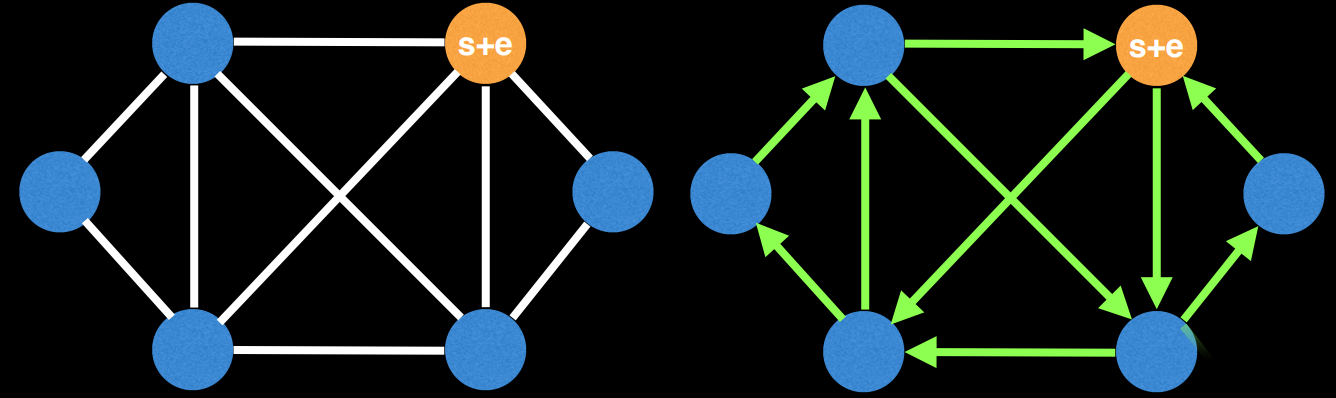
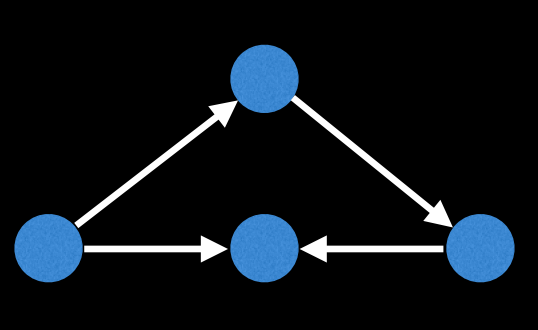
다음과 같이 그래프가 오일러 회로를 갖지 않는 경우도 존재한다. 일반적으로 오일러 경로가 없는 경우거나 오일러 경로가 존재하지만, 시작과 끝점이 다른 경우이다.

오일러 경로는 오일러 회로일 수도 있지만, 시작 정점과 끝 정점이 다른 경우도 포함하므로 오일러 회로가 아닐 수도 있다. 오일러 회로를 이용한다면 정해진 단어 집합에서 모든 단어를 끝말잇기로 연결하는 예제나 가진 항공권을 모두 이용하는 여행 경로를 계획하는 예제 등등 현실 세계에서의 많은 문제도 해결할 수 있다.
오일러 경로의 존재여부 확인
어떤 그래프를 줬을 때, 오일러 경로의 존재 여부를 확인하려면 어떻게 해야 할까?
오일러 경로의 존재 여부를 확인하기 위해 두 가지를 확인해야 한다.
1. 그래프의 간선이 하나의 컴포넌트로 연결되어 있는지?
2. 그래프 간선의 각 정점에 대한 차수
분리된 컴포넌트에서의 오일러 경로
먼저 그래프가 둘 이상의 컴포넌트로 분리되어 있다고 생각해보자.
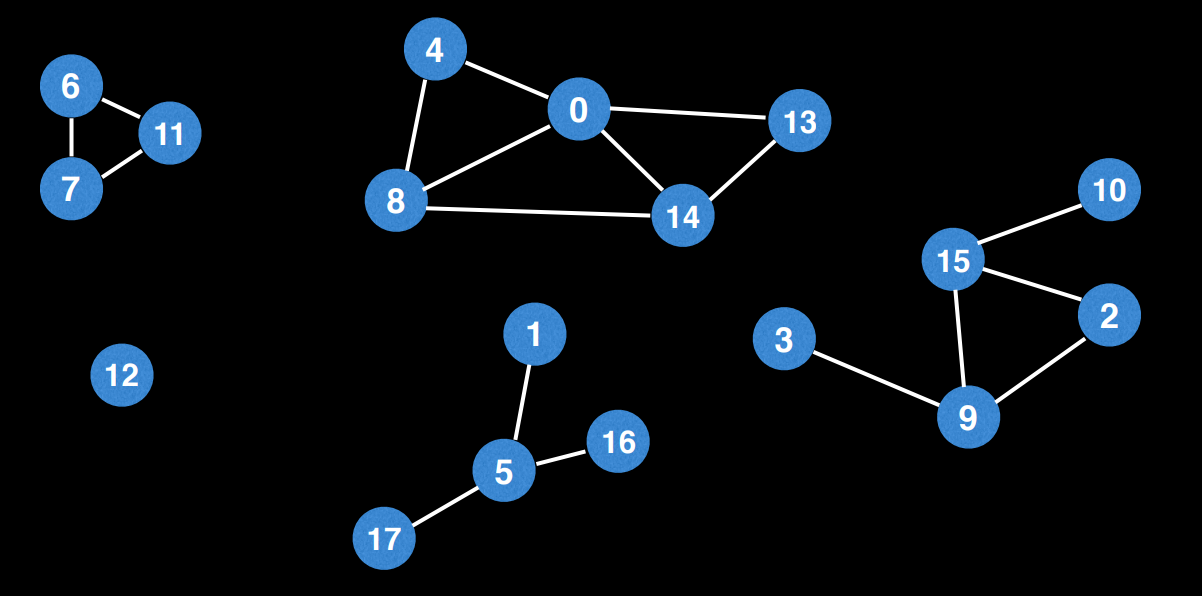
애초에 그래프가 이렇게 분리된 형태라면 모든 간선을 잇는 하나의 경로를 찾는 것은 불가능할 것이다. 위와 같은 그래프에서는 오일러 경로를 찾을 수 없겠지만, 그렇다면 모든 분리된 그래프에서는 오일러 경로를 찾을 수 없는 것일까?
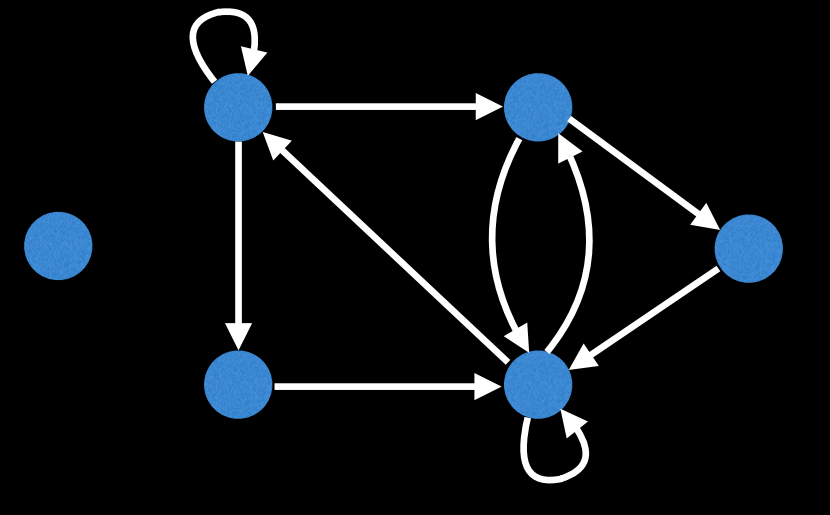
다음 그래프를 보자.

이처럼 그래프의 컴포넌트가 여러 개로 분리되어 있더라도, 다른 컴포넌트들이 간선을 포함하지 않는다면 모든 간선을 포함하는 컴포넌트 속에서 오일러 경로가 존재하게 된다. 실제로 문제 풀이를 하는 경우에도 이와 같은 상황에 대한 예외처리를 빠짐없이 해주어야 할 것이다.
그래프 차수와 오일러 경로 (무향 그래프)
먼저 무향 그래프에서 오일러 경로에 대해 생각해보자.
오일러 경로에서는 시작 정점과 끝 정점이 다른 경우와, 같은 경우(오일러 회로)로 나뉜다고 했다.
1. 시작 정점과 끝 정점이 같은 경우
간선이 있는 그래프에 오일러 회로가 존재하려면, 시작 정점은 나가는 간선을 가질 것이다. 그리고 회로는 어떤 경로를 거쳐서 다시 시작 정점으로 돌아와야 하기 때문에 반드시 들어오는 간선도 가질 것이다. 물론 나가는 간선이 여러 개가 있을 수 있겠지만, 그 수만큼 들어오는 간선을 반드시 갖고 있어야 다시 시작 정점으로 돌아올 수 있다. 그리고 이러한 특징은 중간에 거쳐 가는 모든 정점에도 동일하게 해당한다. 중간 정점들도 외부로부터 들어오는 간선을 갖지만 결국 회로의 최종 정점은 시작 정점이기 때문에, 들어오는 간선 수 만큼 나가는 간선을 갖고 있어야 하기 때문이다. 그러므로 오일러 회로가 존재하려면 모든 정점의 차수가 짝수여야 한다는 결론을 내릴 수 있다.
2. 시작 정점과 끝 정점이 다른 경우
오일러 회로가 아닌 오일러 경로의 경우는 어떨까?
사실 오일러 경로의 경우도 시작 정점과 끝 정점은 정해져 있기 때문에, 중간에 거쳐 가는 정점들은 오일러 경로와 같이 들어오는 간선만큼 나가는 간선이 있어야 한다. 하지만 시작 정점과 끝 정점은 조금 다르다. 시작 정점의 경우 출발지로서 하나의 간선을 필수로 갖고, 몇 번 더 거쳐 가게 되는 경우 들어오는 간선 개수만큼 나가는 간선 개수가 추가되므로 홀수개의 간선을 갖게 된다. 그리고 끝 정점의 경우는 도착지로서 하나의 간선을 필수로 갖고, 몇 번 거쳐 가게 되는 경우 들어오는 간선 개수만큼 나가는 간선 개수가 추가되므로 홀수개의 간선을 갖게 된다. 그러므로 시작 정점과 끝 정점이 다른 경우 오일러 경로가 존재하려면 2개의 정점의 차수가 홀수이고, 나머지 정점들의 차수는 짝수개여야 한다.
그래프 차수와 오일러 경로 (유향 그래프)
다음으로 방향 그래프에서 생각해보자.
방향 그래프에서는 차수에 대해 정리할 때, 들어오는 차수와 나가는 차수를 따로 구분하여 이용한다.
그러므로 기본적인 오일러 경로와 회로의 특성은 무향 그래프와 비슷하지만, 정의 방법이 조금 달라진다.
1. 시작 정점과 끝 정점이 같은 경우 (방향 그래프)
간선이 있는 그래프에서 시작정점은 나가는 간선을 갖겠지만 그 수만큼 들어오는 간선을 갖기 때문에 시작정점의 입력 차수와 출력 차수는 같아야 한다. 또한 중간에 거쳐 가는 정점들도 들어오는 간선 수 만큼 나가는 간선 수를 갖기 때문에 입력 차수와 출력 차수가 같아야 한다. 즉, 모든 정점의 입력 차수와 출력 차수가 같아야 오일러 회로가 존재한다고 할 수 있다.
2. 시작 정점과 끝 정점이 다른 경우 (방향 그래프)
시작 정점의 경우 출발을 위한 간선을 갖기 때문에 최소 하나의 출력 차수를 갖게 된다. 만약 시작 정점에 다시 방문하는 상황이라면 들어오는 간선만큼 나가는 간선이 존재해야 한다. 그러므로 시작 정점의 출력 차수는 입력 차수보다 1 크다. 끝 정점의 경우 도착을 위한 간선을 갖기 때문에 최소 하나의 입력 차수를 갖게 된다. 만약 끝 정점에서 다시 나가는 상황이 생긴다면 그 횟수만큼 들어오는 간선이 추가되어야 한다. 그러므로 끝 정점의 입력 차수는 출력 차수보다 1 크다.
완전히 간선이 없는 상황까지 생각한다면 최종적으로 다음과 같이 정리할 수 있다.
| 오일러 회로 | 오일러 경로 | |
| 무향그래프 | 모든 정점의 차수가 짝수이다. | 오일러 회로이거나, 2개의 정점의 차수가 홀수이고 나머지 정점의 개수는 짝수개이다. |
| 방향그래프 | 모든 정점의 indegree와 outdegree가 같다. | 최대 1개의 정점에 대해, outdegree - indegree = 1 이고 최대 1개의 정점에 대해, indegree - outdegree = 1 이고 그 외 모든 정점은 indegree와 outdegree가 같다. |
예제

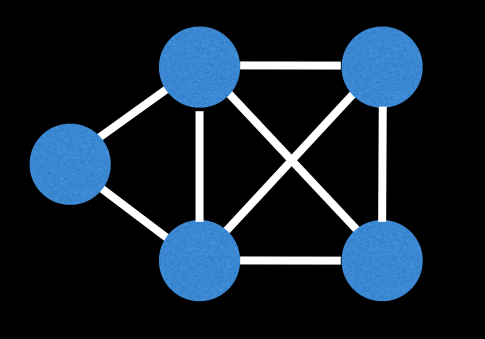

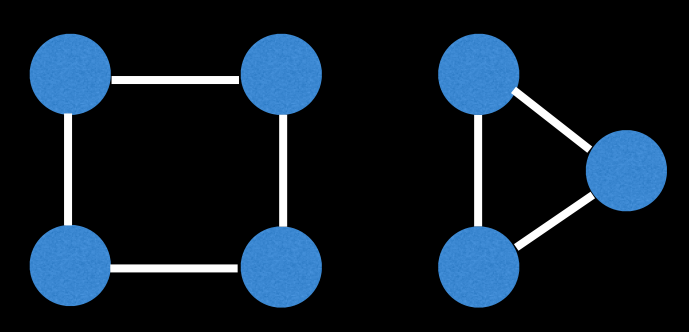

DFS를 이용한 오일러 회로, 오일러 경로 생성
오일러 경로를 실제로 구현할 때에는 주의해야 할 점이 있다. 오일러 경로는 기본적으로 무향 그래프나 방향 그래프에서 존재하지만, 이 그래프들은 동시에 다중 그래프이기도 하다. 즉 하나의 정점에서 똑같은 정점으로 나가는 여러 개의 간선이 존재할 수도 있다는 의미이다. 그렇기 때문에 그래프를 표현할 때, 값으로 가중치 값 대신 간선의 개수를 저장하도록 표현한다.
const int N = 6;
vector<vector<int>> multigraph =
{
{ 0, 1, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 0, 0 },
{ 1, 0, 0, 2, 1, 0 },
{ 0, 1, 2, 0, 0, 1 },
{ 0, 0, 1, 0, 0, 1 },
{ 0, 0, 0, 1, 1, 0 }
};
먼저 방향그래프에서 오일러 회로, 경로를 찾는 알고리즘을 작성해보자.
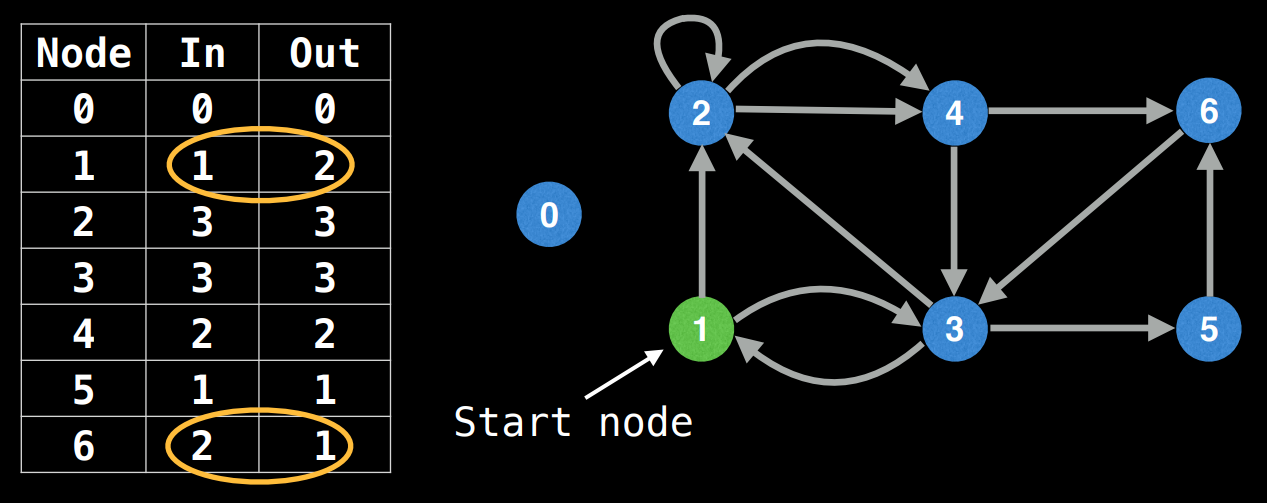
오일러 회로, 오일러 경로를 찾기 위해서는 먼저 그래프의 입력차수(Indegree)와 출력차수(Outdgree)를 생성해야한다.
insooneelife/AlgorithmTutorial
알고리즘 튜토리얼. Contribute to insooneelife/AlgorithmTutorial development by creating an account on GitHub.
github.com
입력차수와 출력차수가 생성되었다면 이를 통해 오일러 회로인지 오일러 경로인지를 판단할 수 있다.
먼저 모든 indegree와 outdegree가 같은지 판단하여 오일러 회로 여부를 확인한다.
// 방향 그래프에서 euler circuit이 성립하려면 모든 노드에 대해 indegree와 outdegree가 같아야한다.
bool CheckEulerCircuit(const vector<int>& indegree, const vector<int>& outdegree)
{
return indegree == outdegree;
}
그 외의 경우라면, 두 개의 정점에 대해 outdegree - indegree = 1, indegree - outdegree = 1 이면서 그 외 정점들의 indegree와 outdegree가 같은지 판단하여 오일러 경로 여부를 확인한다.
bool CheckEulerTrail(
const vector<vector<int>>& graph,
const vector<int>& indegree,
const vector<int>& outdegree,
int& start_node,
int& finish_node)
{
int startcnt = 0;
int finishcnt = 0;
// 시작, 끝 노드는 유일해야함
for (int i = 0; i < indegree.size(); ++i)
{
if (outdegree[i] == indegree[i] + 1)
{
start_node = i;
startcnt++;
}
if (outdegree[i] + 1 == indegree[i])
{
finish_node = i;
finishcnt++;
}
}
if (!(startcnt == 1 && finishcnt == 1))
return false;
// 그 외에는 같아야함
for (int i = 0; i < indegree.size(); ++i)
{
if (i == start_node || i == finish_node)
continue;
if (outdegree[i] != indegree[i])
return false;
}
return true;
}
이렇게 회로인지 경로인지가 명확해졌다면 이제 DFS를 이용하여 실제 경로를 찾아보자. 오일러 회로를 찾는 과정과 오일러 경로를 찾는 과정은 같다. 다만, 오일러 경로의 경우 시작점과 끝점이 정해져 있기 때문에, 차수 계산을 통해 특정 시작점에서 탐색을 시작해야 한다는 점이 다르다.
기본적으로 오일러 경로를 찾기 위해서는 간선에 대해 DFS 탐색을 수행한다. 오일러 경로는 한 정점을 여러 번 방문하는 경우도 충분히 생길 수 있기 때문에, 기존의 정점 방문 기록 방식과 달리 간선 방문을 체킹하는 방식으로 구현해야 한다. 그러므로 DFS 탐색 과정 중에 이미 거쳐 간 간선을 하나씩 제거하도록 한다. 또한 DFS를 계속 수행해나가기 위한 조건으로 현재 정점에서 나가는 간선이 있는지를 판단하도록 해야 한다. 그리고 이 탐색 과정에서 백트래킹을 할 때 경로를 저장하며 돌아오도록 하면 쉽게 오일러 경로를 얻을 수 있다.
다음 그림을 보자.
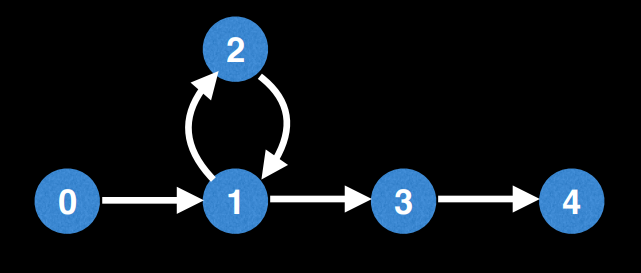
먼저 DFS를 통해 탐색할 수 있는 정점까지 탐색을 수행한다.

백트래킹을 하는 과정에서 경로를 저장한다.
euler : [4, 3]
아직 탐색되지 않은 간선에 대해 다시 탐색을 시작한다.

다시 백트래킹 하며 방문 정점을 저장한다.
euler : [4, 3, 1, 2]
euler : [4, 3, 1, 2, 1, 0]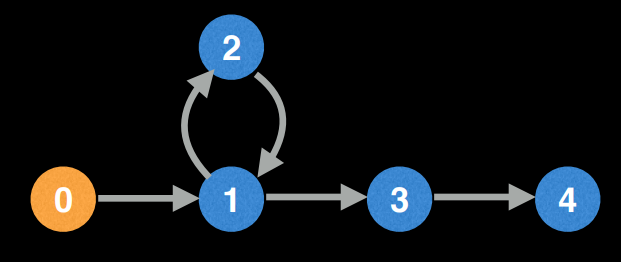
이제 만들어진 역추적 경로를 역순으로 수정하면 오일러 경로를 찾을 수 있다.
euler : [0, 1, 2, 1, 3, 4]모든 간선을 제거할 때까지 탐색을 진행하기 때문에 오일러 경로를 찾는데 필요한 시간복잡도는 O(E)가 된다. 오일러 회로의 경우도 같은 방법으로 경로를 찾을 수 있다. 다만, 오일러 회로의 경우는 시작 정점과 끝 정점이 따로 정해져 있지 않기 때문에 어떤 정점을 주더라도 상관없다.
무향 그래프에서의 오일러 경로, 오일러 회로에 대한 구현도 방향 그래프와 크게 다르지는 않다. 크게 두 가지만 수정해주면 된다.
1. 무향 그래프에서의 오일러 경로, 오일러 회로의 존재 여부 확인
2. 그래프에서 간선을 제거할 때 양쪽 간선을 모두 제거
다음 링크는 무향 그래프에서의 오일러 경로, 오일러 회로를 구현한 코드이다.
https://github.com/insooneelife/AlgorithmTutorial/blob/master/Algorithm/Sources/EulerPath/1-Euler-Path.cpp
insooneelife/AlgorithmTutorial
알고리즘 튜토리얼. Contribute to insooneelife/AlgorithmTutorial development by creating an account on GitHub.
github.com
다음 링크는 유향 그래프에서의 오일러 경로, 오일러 회로를 구현한 코드이다.
https://github.com/insooneelife/AlgorithmTutorial/blob/master/Algorithm/Sources/EulerPath/2-Directed-Euler-Path.cpp
insooneelife/AlgorithmTutorial
알고리즘 튜토리얼. Contribute to insooneelife/AlgorithmTutorial development by creating an account on GitHub.
github.com
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [Algorithm] 유향 비순환 그래프 (0) | 2021.06.26 |
|---|---|
| [Algorithm] 최단 경로 (0) | 2021.06.26 |
| [Algorithm] 부분합 (0) | 2021.06.19 |
| [Algorithm] 그래프 (0) | 2021.06.19 |
| [Algorithm] 구간트리 (0) | 2021.06.12 |
