[Algorithm] 백트래킹

백트래킹

백트래킹(Backtracking)은 컴퓨터 계산 문제, 특히 제약 충족 문제(Constraint Satisfaction Problem)에 대한 해결방법을 찾기 위한 일반적인 알고리즘으로, 솔루션에 대한 후보를 점진적으로 구축하고 후보가 유효하지 않다면 해당 후보를 포기하고 퇴각하여 이전 단계부터 다른 선택을 해나가는 방식으로 동작한다. 다음 문제들을 보자.

 

스도쿠

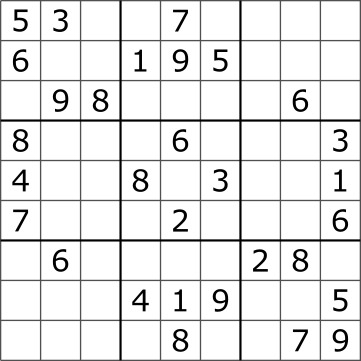
스도쿠는 아래 그림과 같이 가로, 세로 각각 9개씩 총 81개의 작은 칸으로 이루어진 정사각형 판 위에서 이뤄지는데, 게임 시작 전 일부 칸에는 1부터 9까지의 숫자 중 하나가 쓰여 있다.

나머지 빈칸을 채우는 방식은 다음과 같다.

1. 각각의 가로줄과 세로줄에는 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.
2. 굵은 선으로 구분된 3 x 3 정사각형 안에도 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.

 

일반적인 상태 공간 탐색을 이용하여 이 문제에 접근해보자. 먼저 상태 데이터를 정의해야 할 것이다. 스도쿠에서 가능한 상태는 어떻게 표현될 수 있을까? 스도쿠 게임판에서 정적인 부분을 제거하더라도 모든 공백에는 1부터 9 사이의 숫자 혹은 공백이 들어가야 할 것이다. 위에 그림만 봐도 공백의 개수가 최소 20개는 될 것인데, 대충 어림잡아도 10 ^ 20으로 메모리에 담을 수 없을 정도의 크기이다. 이렇게 많은 상태를 너비 우선 탐색과 같은 탐색 방법으로 탐색한다면 큐에서 메모리 초과 문제가 발생할 것이다.

또한, 이 문제는 어떤 상태에서 값을 결정했을 때, 결정된 그 값으로 인해 행, 열, 직사각형 공간에 대해 새로운 조건이 생성되고 그 주변의 값들의 범위가 축소된다는 특징을 갖는다. 이처럼 특정 조건들이 변수를 제약하는 상황에서 모든 조건을 만족시키는 변수의 쌍을 구하는 문제들을 제약충족 문제라 부른다. 이런 제약충족 문제들은 상태 데이터 크기가 직면한 상태에 적용된 조건들에 따라 너무 넓게 분포되므로 데이터를 타이트하게 표현하기 어렵다. 그렇기 때문에 이런 형태의 문제들은 상태 데이터를 직접 설계하는 방향보다는 2차원 배열 게임판과 같은 거대한 공유 상태 데이터를 갖고 이 배열에서 동적으로 변하는 델타값을 위한 파라미터만 이용하는 형태로 구현한다. 또한 탐색 방법도 너비 우선 탐색보다는 백트래킹을 이용한다.

 

가능한 행동은 어떤 것들이 있을까?

이 부분은 문제를 어떻게 설계하느냐에 따라 다를 것이다.

만약 위의 그림에서 맨 윗줄 왼쪽부터 오른쪽 아래까지의 모든 공백의 위치를 순서대로 나열한 배열이 있다고 한다면,

배열의 x번째 위치에 해당하는 공간에 넣을 수 있는 모든 숫자를 넣어보는 것들이 가능한 행동들이 될 것이다.

 

N-Queen

Queen은 가로, 세로, 양쪽 대각선 모두 공격이 가능하다.

8 x 8 체스판 위에 8개의 Queen을 서로 공격할 수 없게 배치해야 한다.

가능한 모든 경우의 수를 구하시오.

가능한 해 중 하나

이 문제에서 가능한 상태는 어떻게 표현될 수 있을까?

각 퀸은 한 줄에 하나밖에 배치될 수 없기 때문에,

체스판을 모두 사용할 필요 없이 각 라인에 대한 배열을 상태로 이용할 수 있을 것이다.

각 라인에는 퀸이 위치한 위치 정보 + 공백 정보로 9가지 숫자가 이용될 것이다.

vector<int> lines(8);

이렇게 상태를 잡게 되면 9 ^ 8 정도 크기로 메모리에 담기에는 큰 크기이다. 이 문제도 잘 생각해보면 어떤 행동을 선택했을 때, 그 행동이 다음 상태의 크기에 영향을 주는 제약충족 형태의 문제이다. 그러므로 조건들이 중첩된 상태에서 실제 가능한 경우의 수는 9 ^ 8보다 훨씬 작을 것이고, 굳이 상태를 데이터화 시켜서 해결하는 것보다는 게임판을 공유 데이터로 사용하여 변하는 값만 기록하는 형태로 접근하는 것이 효과적이다. 마찬가지로 너비 우선 탐색보다 백트래킹을 이용하는 것이 좋다.

 

이 문제에서의 행동은 어떻게 정의될 수 있을까?

이 또한 방법을 어떻게 설계하느냐에 따라 다르겠지만, 위에서부터 하나씩 퀸을 배치하는 전략을 취한다고 했을 때,

현재 상태의 라인에서 선택할 수 있는 모든 칸에 배치해볼 수 있을 것이다.

 

Map Coloring 문제

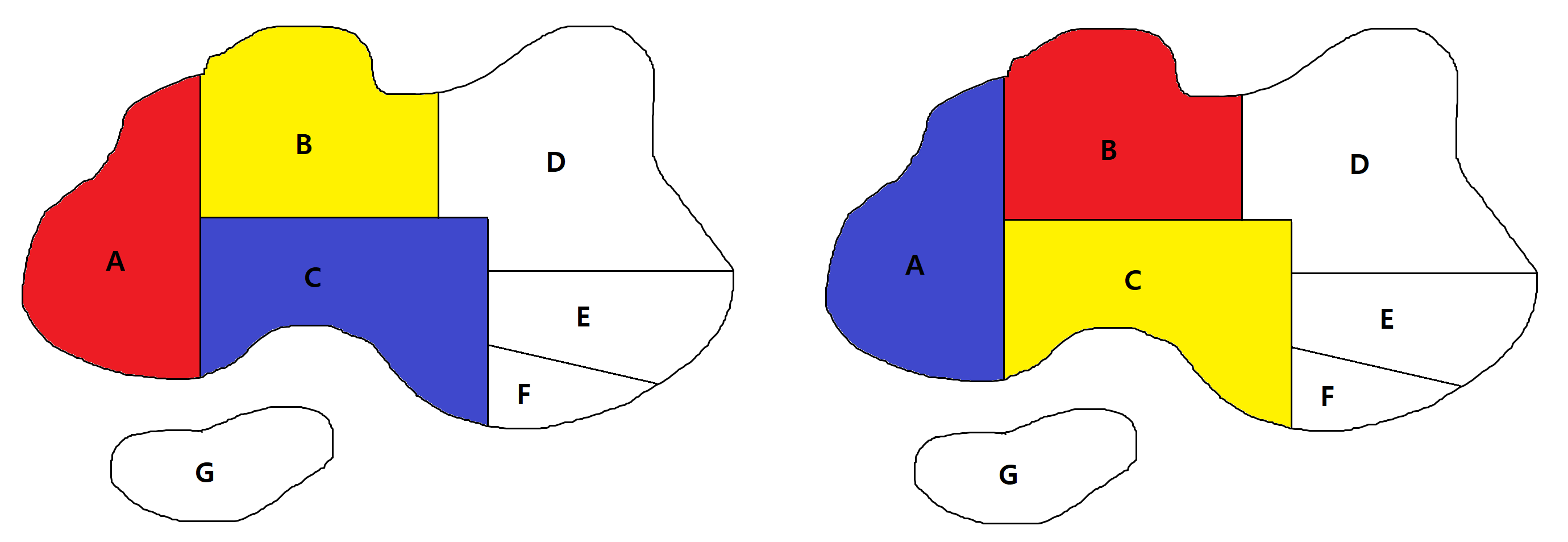
Map Coloring 문제는 지도 위에 구분된 영역을 서로 다른 색상을 이용하여 칠하는 모든 경우의 수를 구하는 문제이다. 아래 그림을 예로 들어보자. 색상은 빨강, 파랑, 노랑 세 가지가 주어졌다고 가정한다. 먼저 A 위치에 빨간색을 칠하면 B와 C 위치에는 빨간색을 칠할 수 없다. 만약 A 위치를 파란색으로 칠한다면 B, C 위치를 파란색으로 칠할 수 없을 것이다. 이처럼 어느 한 색상을 한 위치에 선택하는 순간 그 주변에 위치한 색상의 후보에도 제한조건이 생기게 된다. 이 문제 역시 유명한 제약충족문제 중 하나이다.

이 문제를 풀려면 어떻게 해야할까?

먼저 위 지도를 그래프 형태로 다시 표현해보자. 그 후 이 그래프에서 시작정점를 정해서 사용할 수 있는 모든 색을 하나씩 칠해보며 카운팅하면 문제를 해결할 수 있을 것이다.

 

 

 

 

탐색 방법

깊이 우선 탐색(DFS)

깊이 우선 탐색은 시작 노드부터 최대한 멀리 있는 노드까지 탐색하고, 

더 탐색할 노드가 없으면 한 칸 위로 올라와 다시 최대한 탐색하는 형태로 진행한다.

다음과 같은 순서로 노드를 방문하게 된다.

노드 방문 순서
0 1 3 4 2 5 6

 

일반적으로 스택이나 재귀로 구현된다. 위 트리를 양방향 그래프로 만들고 구현해보자. 각 방문된 정점에 대해 인접 행렬에서 연결된(값이 1) 정점들에 대해 재귀적으로 탐색을 수행한다. 또한 이미 방문 된 노드를 다시 방문하지 않도록 하기 위해, 방문 배열에 기록한다.

 

소스코드 (DFS)

https://github.com/insooneelife/AlgorithmTutorial/blob/master/Algorithm/Sources/Graph/1-DFS-adjmatrix.cpp

insooneelife/AlgorithmTutorial

 

 

미로찾기 문제

다음과 같은 미로가 주어졌을 때,

이 미로가 (0, 0) 위치에서 (N - 1, N - 1) 위치로 도달 가능한지 확인하는 알고리즘을 작성해보자.

const int N = 6;
int arr[N][N] =
{
    1,0,1,1,1,1,
    1,0,1,0,1,0,
    1,0,1,0,1,1,
    1,1,1,0,1,1,
    0,0,1,0,0,1,
    0,0,1,1,0,1
};

 

 

소스코드 (미로찾기)

https://github.com/insooneelife/AlgorithmTutorial/blob/master/Algorithm/Sources/Backtracking/1-DFS-Maze.cpp

insooneelife/AlgorithmTutorial

 

 

백트래킹 (DFS + 가지치기)

백트래킹은 DFS보다는 좀 더 넓은 개념이지만,

상태 공간탐색에서는 기본적으로 DFS와 같은 형태로 구현되며, 추가로 가지치기를 병행하는 개념으로 통용된다. DFS의 경우 명시적으로 정형화된 트리의 노드를 탐색하는 반면, 백트래킹은 조건에 맞게 암시적인 상태트리를 탐색한다는 점에서 차이가 있다. (트리가 있어서 탐색한 것이 아니라, 탐색하고 보니 트리였다.)

백트래킹을 하기 위해서 먼저 알아둬야할 개념들이 있다. 다시 N-Queen 문제를 예로 들어보자.

 

1. 선택할 수 있는 행동들과 조건에 따른 가지치기

N-Queen 문제를 예로 들자면, 직면한 현재 상태에서 퀸을 놓을 수 있는 모든 위치에 한 번씩 놓아본다.

퀸을 놓은 후에는 그 퀸으로 인해 이동할 수 없는 위치에 대한 정보를 상태 데이터에 기록한다.

이렇게 기록된 정보는 재귀적으로 더 깊어진 상태에서의 탐색 과정에서 행동에 대한 가지치기를 위해 사용될 것이다.

 

2. 상태 데이터의 공유

N-Queen 문제에서의 상태 데이터는 너무 크기 때문에 구조체로 데이터화 시켜서 전달하는 것은 무리가 있다.

그러므로 게임판 자체를 상태 데이터로 생각하되, 이 데이터를 모든 재귀 수준에서 공유하도록 한다.

즉 전역변수나 레퍼런스를 이용한다는 의미이고, 상태 데이터가 공유되기 때문에 메모리나 성능적인 부분에서의 많은 이득을 취할 수 있다.

 

3. 각 행동에 따른 공유 상태 데이터의 변화 및 복구

상태 데이터를 공유하는 점은 메모리, 속도와 같은 성능적인 측면에서 좋고,

재귀적으로 깊어진 상태에서 이전 상태 데이터를 활용할 수 있다는 점에서 기능적으로도 의미가 있다.

하지만 만약 리프 노드까지 방문한 후, 다른 선택지를 다시 탐색해야 하는 상황에는 어떻게 해야 될까?

이전에 낙서 된 상태 데이터에서 탐색을 진행한다면 유효한 해답을 발견하기는 힘들 것이다. 그러므로 하나의 컨텍스트가 시작되기 전에 공유 상태 데이터에 행동에 대해 기록을 했다면, 컨텍스트가 끝난 후에는 공유 상태 데이터에서 그 기록을 이전 상태로 복구시켜주어야 한다.

N-Queen 문제의 코드를 약식으로 작성하면 다음과 같은 형태가 될 것이다.

SetQueen(int line)
    정답인 경우 처리
    
    for 모든 가능한 행동에 대해:
    	게임판 기록 (퀸 정보)
    	SetQueen(line + 1)
    	게임판 복구

 

 

소스코드 (N-Queen)

https://github.com/insooneelife/AlgorithmTutorial/blob/master/Algorithm/Sources/Backtracking/2-Backtracking-NQueen.cpp

insooneelife/AlgorithmTutorial